Uno dei fondamenti dell’analisi statistica è la distribuzione normale. In questo post vedremo cosa è, le sue caratteristiche e il perchè è così importante in questo ambito.
Questo ci permetterà di avvicinarci sempre più alla risposta alla domanda “I valori di glucosio raccolti nei due ospedali differisce realmente?”. Se avete bisogno di rinfrescarvi la memoria, la storia inizia nell’articolo sugli indici di centralità e prosegue in quello sugli indici di dispersione (richiameremo anche altri concetti degli articoli in questione, per questo consiglio di riguardarli).
Distribuzione normale
Una distribuzione è una rappresentazione grafica di come i valori di una variabile si distribuiscono nelle unità statistiche (d’ora in poi soggetti nel nostro caso) che compongono la popolazione (o il campione) a cui fanno riferimento.
In parole povere, è un grafico che ci indica quanti soggetti hanno il valore x, quandi il valore x+1, x+2 ecc ecc. Più precisamente, sull’asse y è espressa la frazione di soggetti con un determinato valore e l’area sottesa dalla curva tra due valori (x1, x2) indica la frazione di soggetti che hanno valori compresi tra x1 e x2.
La distribuzione normale (la famosa distribuzione "a campana") è un particolare tipo di distribuzione, con caratteristiche ben precise:
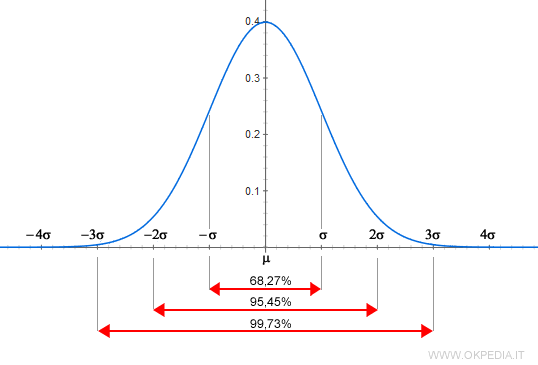
Influenza di media e deviazione standard sulla forma della curva
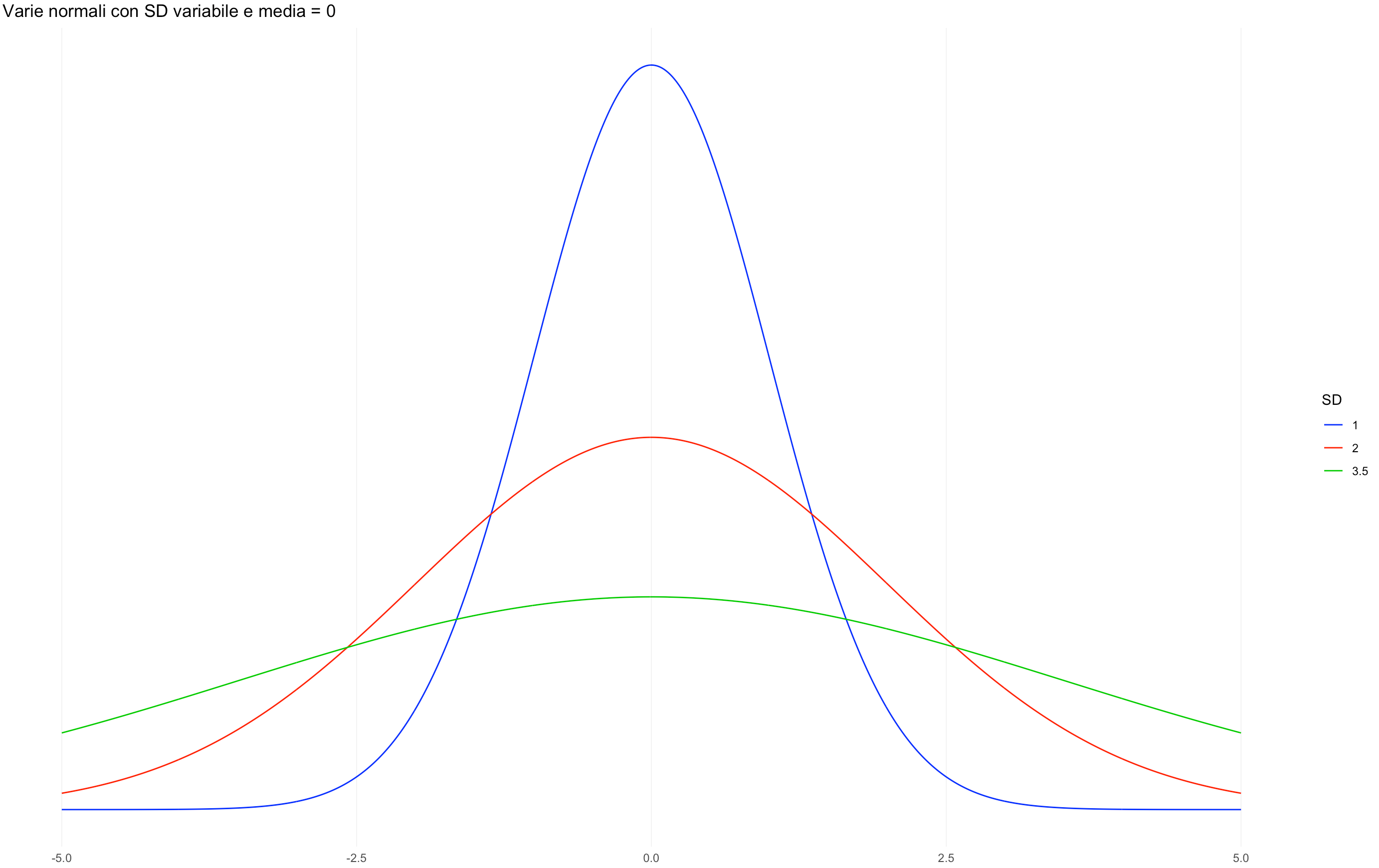
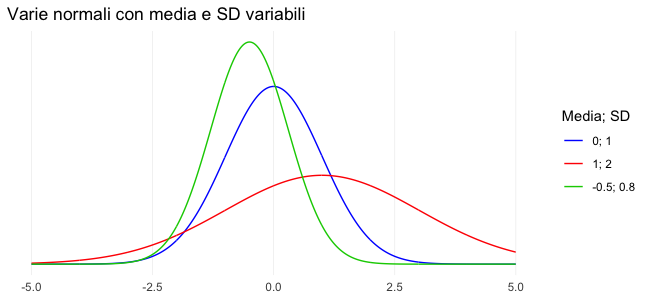
Dal momento che la distribuzione è caratterizzata da solo due indici (media e deviazione standard), la sua forma verrà influenzata dal cambiamento dei loro valori. In particolare, il variare della media sposterà a destra o a sinistra l’intera curva, mentre il cambiamento della deviazione standard “schiaccerà” o “allargherà” la distribuzione.
Vari esempi possono essere visti nelle finestre qui sotto:
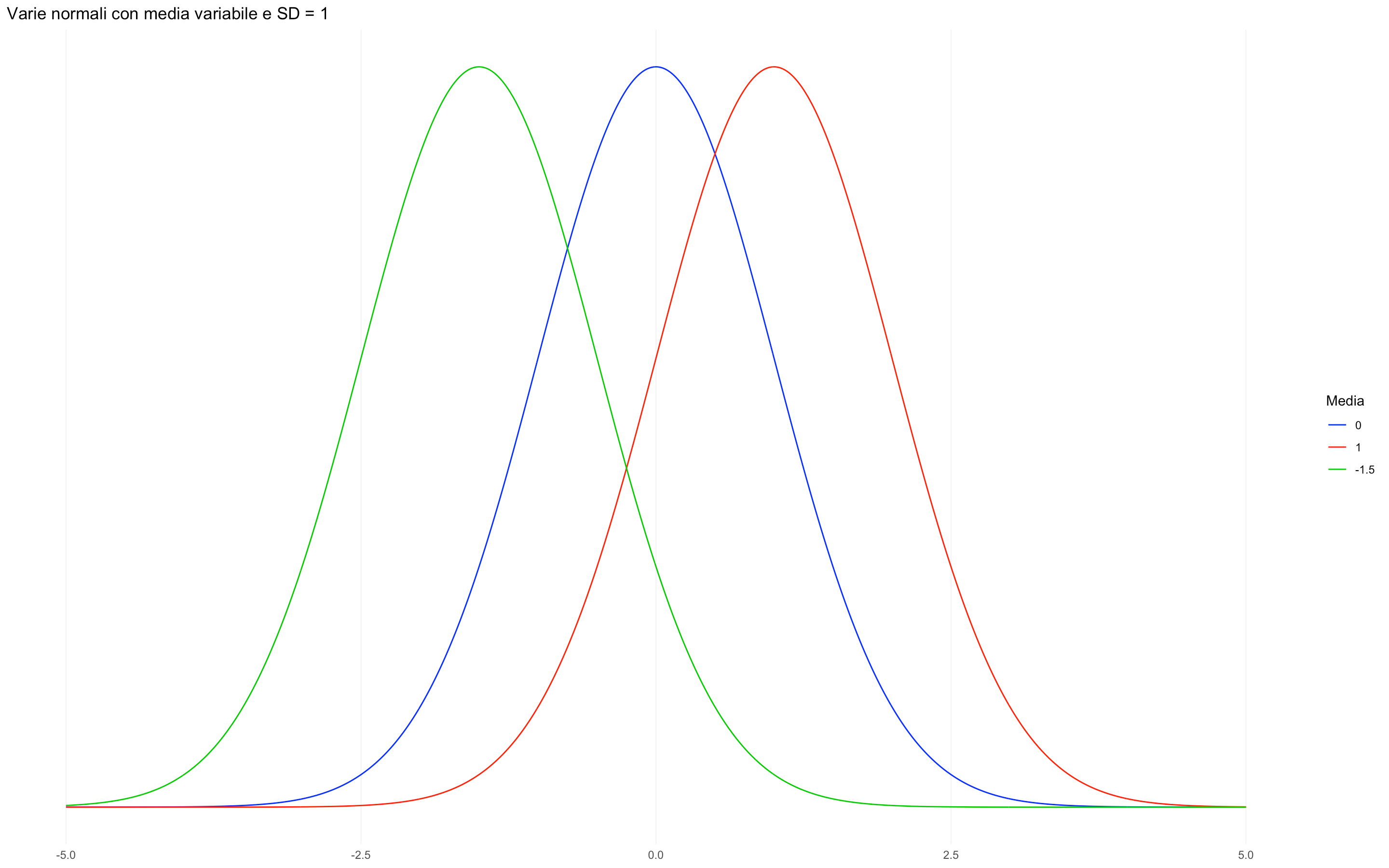
Media variabile
Distribuzione normale standardizzata
C’è una specifica distribuzione normale che in statistica è un vero e proprio pilastro: la distribuzione normale standardizzata. Le sue caratteristiche sono quella di avere una media pari a 0 e una deviazione standard pari a 1 (in simboli ~N(0;1)).
Perchè è un pilastro? I motivi sono 2: la possibilità di calcolare facilmente l’area sotto la curva e la possibilità di trasformare qualsiasi normale in una standardizzata.
Ricavare l’area sotto la curva di una normale standard
Partiamo ricordando che l’area sottesa dalla curva indica la frazione di soggetti che hanno valori compresi tra i due estremi: questi estremi possono essere entrambi numeri reali (per esempio 1 e 2), oppure uno dei due può essere +/- infinito, creando le famose “code” (di sinistra se l’intervallo è (-Inf, X), di destra se invece è (X, +Inf)).
In figura 2 ne vediamo degli esempi.
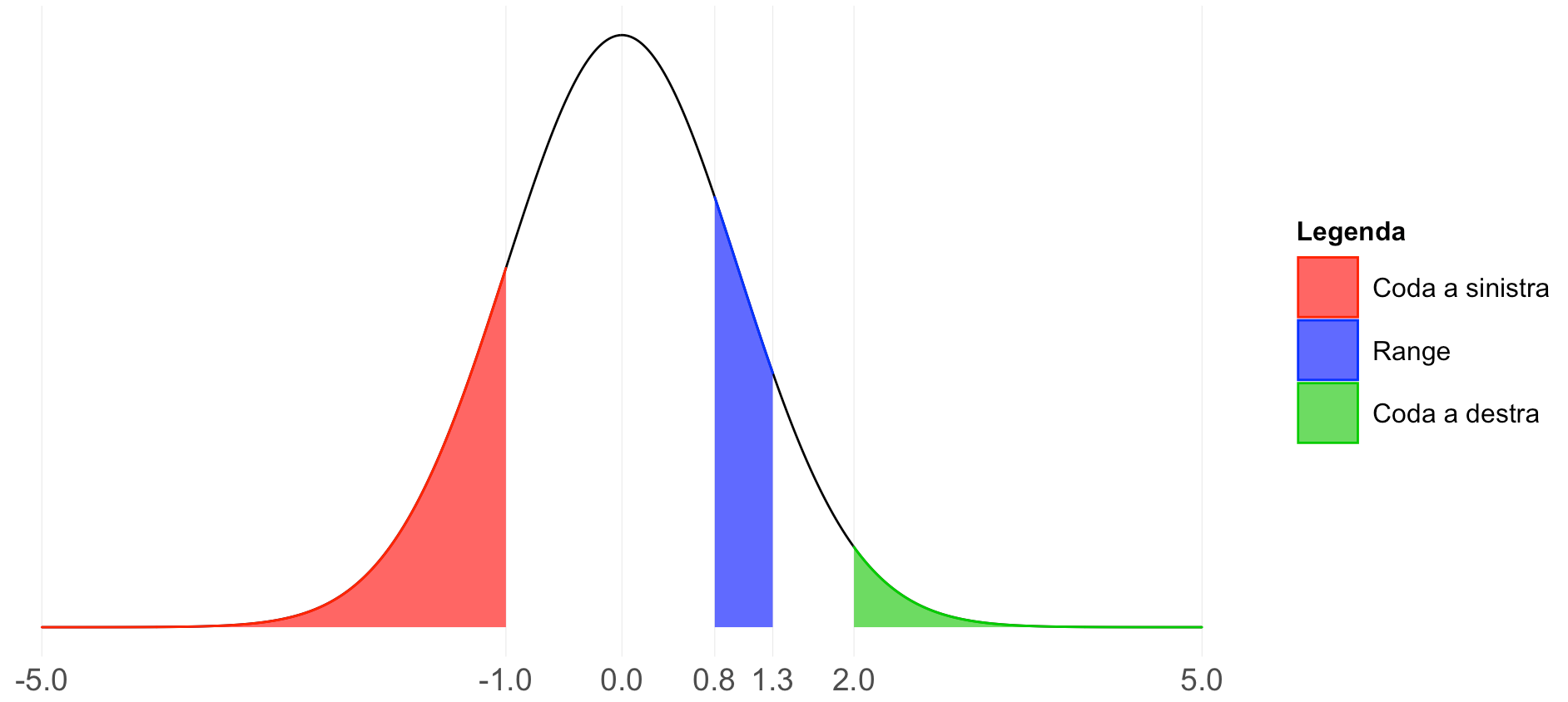
Essendo questa curva ormai ben nota e standardizzata, per ogni valore X è possibile ricavare la coda a sinistra, trovando dunque la frazione di soggetti con valori inferiori ad X. Qui potrete trovare una tabella con i valori.
Come leggerla? L’intestazione delle righe indica i valori di unità e prima cifra decimale mentre quella delle colonne indica la seconda cifra decimale. Incrociando la riga e la colonna corrispondente al valore X (qui chiamato Z-score) si trova la frazione di soggetti che hanno un valore inferiore.
Seguendo l’esempio in figura 2, volendo trovare la frazione di soggetti con un valore inferiore a -1.00 si incrocia la riga -1.0 con la colonna 0.00 e si trova il valore 0.15866; questo significa che circa l'15.9% dei soggetti ha valori inferiori a -1.00 (coda sinistra in rosso).
E se si volesse sapere quelli della coda destra (in verde)? Sapendo che la totalità dei soggetti è rappresentata dalla frazione 1.00, sottraendo a questo valore la coda sinistra rispetto ad X=2.00 si avrebbe il risultato. In questo caso sarebbe 1 - 0.97725 = 0.02275, ovvero circa il 2.2%.
Infine, volendo ricavare la frazione di soggetti appartenenti al range in blu (tra 0.8 e 1.3), si sottrae la coda a sinistra di 0.8 a quella di 1.3, ottendendo così 0.90320 - 0.78814 = 0.11506 (circa l'11.5%).
Standardizzazione di una normale generica
L’altra caratteristica importantissima che rende la normale standardizzata così speciale, è proprio quella di essere standardizzata. Questa curva infatti è il risultato di una normalizzazione (standardizzazione in questo caso) di una qualunque distribuzione normale: se ad ogni valore di una qualsiasi normale si sottrae la media e si divide questo risultato per la deviazione standard, si ottiene una distribuzione con media 0 e SD = 1.
I risultati così ottenuti si chiamano Z-score (ecco che si riprende il termine della tabella). La formula è dunque .
Questo ha una implicazione molto utile: per una qualsiasi normale, è possibile calcolare l’area sotto la curva (che sia coda o range) trasformando i valori in Z-score e usando la tabella.
Esempio:
Si sa che in una popolazione l’altezza si distribuisce secondo una normale con media 171 cm e deviazione standard 23 cm. Quale frazione di questa popolazione è alta meno di 150 cm? E più di 210?
Per rispondere alla prima domanda, si deve trasformare 150 nel corrispettivo Z-score e usare la tabella. Dunque, . Approssimando a -0.91, nella tabella si trova il valore 0.18141; dunque, la risposta è circa 18%.
Per la seconda risposta si fa la stessa cosa: . Approssimando a 1.70, dalla tabella si ricava 0.95543. Bisogna ricordarsi che la domanda chiedeva la coda destra, mentre qui c’è il valore della cosa sinistra; sottraendo questo valore ad 1.00 troviamo la vera risposta alla domanda, ovvero 1 - 0.95543 = 0.04457 (4.4%).
L’importanza
Ora che abbiamo visto le caratteristiche e le proprietà della distribuzione normale, cerchiamo di capirne la sua importanza: come abbiamo detto, la distribuzione normale è caratterizzata da due valori (media e deviazione standard) che riescono a descrivere in maniera abbastanza esaustiva il campione. Sappiamo infatti il valore medio e, di conseguenza, la mediana; siamo a conoscenza di come sono distribuiti i valori attorno al valore medio, grazie alla deviazione standard.
Abbiamo dunque le due caratteristiche fondamentali per avere una idea del campione e dei suoi valori.
Inoltre, con la possibilità di standardizzare qualunque distribuzione normale, siamo in grado di calcolare la frazione di un campione molto ampio (perchè bisogna ricordarsi che qui si parla di campioni ampi) che ha valori maggiori o minori rispetto ad una soglia.
Conclusioni
Oggi abbiamo visto cosa è la distribuzione normale e le sue peculiarità. È una delle distribuzioni più famose in statistica e ci aiuterà ad avvicinarci alla risposta alla domanda “I valori di glucosio raccolti nei due ospedali differisce realmente?". Scopriremo il perchè in un prossimo post.
Stay tuned!